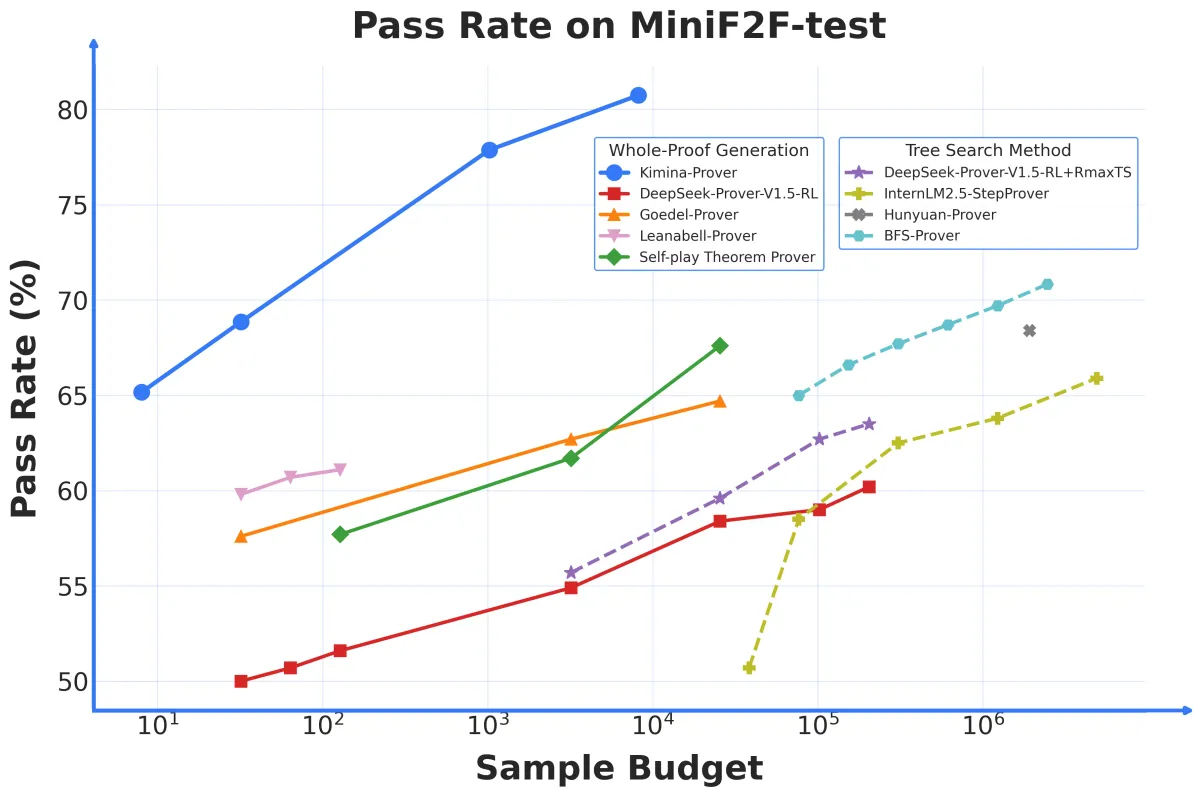
Mathematical theorem proving has long been a playground for AI researchers, pushing the boundaries of formal reasoning and symbolic logic. Today, a fresh contender named Kimina-Prover Preview, developed by the collaboration of the Moonshot AI team (known as 月之暗面 Kimi) and Numina, has stormed the leaderboard by achieving an unprecedented 80.7% pass rate on the MiniF2F benchmark. This is a whopping 10.6% improvement over the previous state-of-the-art (SOTA), setting a new bar for AI models tackling formal mathematics.
Kimina-Prover Preview isn't just about raw scores; it embodies a thoughtful fusion of scale, training innovation, and reasoning style that collectively elevate its capabilities.
First off, the model operates in Lean 4, a modern proof assistant language favored for formal verification tasks. Unlike many earlier systems that relied heavily on complex heuristics like Monte Carlo tree search or value functions, Kimina-Prover leans into reinforcement learning (RL) to generate whole proofs in one go—without feedback loops during training or inference. This approach borrows from its predecessor Kimi k1.5 but pushes further, demonstrating that sophisticated theorem proving can be achieved with a streamlined, end-to-end methodology.
One of the standout technical feats is the model’s size and context window. At 72 billion parameters, Kimina-Prover is notably larger than previous neural theorem provers, and this scaling correlates directly with performance gains—a trend that had been elusive in this niche until now. Moreover, the model handles context windows up to 32,000 tokens, the longest yet attempted in neural theorem proving, enabling it to reason over lengthy and complex proofs more effectively.
But size and scale alone don’t tell the whole story. The team behind Kimina-Prover also introduced a novel Formal Reasoning Pattern, a reasoning style that seeks to bridge the gap between the rigorous, mechanical nature of formal verification and the more intuitive, human-like mathematical reasoning. This design choice likely contributes to the model's ability to generate proofs that are not only correct but also resonate with the kind of reasoning mathematicians employ informally.
In a refreshing move, the Kimina-Prover team has open-sourced distilled versions of their reinforcement learning models and an autoformalization model on Hugging Face, inviting the community to explore, validate, and build upon their work. The GitHub repository also includes all proofs discovered during the MiniF2F tests, promoting transparency and reproducibility.
Interestingly, Kimina-Prover's rigorous reasoning helped uncover at least five incorrectly formalized problems within the MiniF2F-test dataset itself. The team released a rectified version of this benchmark, underscoring how advanced AI can contribute not only by solving problems but by refining the very datasets used to measure progress.
Kimina-Prover Preview’s achievement—an 80.7% pass rate on MiniF2F—surpasses notable predecessors like BFS-Prover (72.9%) and other contenders including Hunyuan-Prover and Leanabelle-Prover by a significant margin. Its high sample efficiency means it performs impressively even with limited proof attempts, hitting around 68.85% pass rate at 32 attempts and 65.16% at just 8.
This breakthrough signals a maturation in neural theorem proving: scaling up model size, extending context windows, and innovating in training methodology aren’t just incremental improvements—they can unlock qualitatively new capabilities. With Kimina-Prover, the dream of AI systems that can rigorously and intuitively assist or even independently verify complex mathematics edges closer to reality.
For those interested in diving deeper or experimenting with the model, the team’s GitHub repository provides a treasure trove of resources, from model checkpoints to corrected datasets and proof artifacts.
